The Fourth Part of Logick
of Method, or an orderly disposition of our thoughts.
Cap. 1. of the general method of knowing.
Althô perhaps there may be some men of so sagacious a witt, that without difficulty they may peirce into difficult things, and know how to solve abstruse questions, yet will none ever obtain certain knowledge, unless they first know how their mind is to be directed, and what order it ought to observe: and therefore method is necessary, or some doctrine whereby the mind may be helped in searching for truth; and may free it self from error, confusion and obscurity.
This method may be defined, such a series or disposition of things to be handled as may be most accomodated to the capacity of the Learner.
That our minds may be sufficiently helped here, & so knowledge obtained 3 things are requisites
- 1. that the thing proposed be clearly and distincly perceived.
- 2. that we pass a right Judgment on the things thus rightly perceived. &c
- 3. that we lay up in our memories truths thus discovered, or those things which we have rightly perceived and Judged of. by the due observance of these 3 precepts we may help all the infirmities of our minds. for since the ostacles of knowledge are either, 1—Too great præcipitance of mind, A clear & distinct perception takes away that; 2—Error or doubt: they are removed by this right Judgment, or, 3—oblivion and forgetfulnesse: that likewise will be prevented by this memory or Remembrance.
A clear and distinct perception will be much furthered, if removeing all precipitance, we attend heedfully to the thing proposed, and view it as it were with internal eyes; to which it will conduce much if we consider of but one thing at once, for plenty of objects does certainly breed confusion.
That we may duely observe the 2d precept, is requisite evermore that knowledge preceed Judg: and that simple terms be placed before such as are complex and if at any time it happens, that we are brought into doubt concerning any thing, we shall readily escape error, if we suspend Judgment, affirming or denying nothing til more light is brought, and all obscurities therefore removed.
Yet we are not to think that all things which are true do carry the same certainty with them; for some things are only contingently true, i.e. they might be false, thus, if I Judge that a man is pious because he frequents the church, lives in the practice of prayer &c which things ordinarily are sufficient for me to Judge a man pious by, and yet it is possible that this man may be void of all true piety notwithstanding these his actings, somethings are altogether certain and true; as propositions of eternal verity, bis quatore sunt octo, Ternarius est numerus &c:103
But because it availes little or nothing to know the nature of things, unless we withall Remember them, we are therefore to Learn how things understood by us may be committed to memory, and so to be Imprinted on it as to be hardly lost or removed thence: and this will readily be attained if we follow the order of our method, i.e. if we commit nothing to memory but what has been found out and rightly Judged of by us: for we dayly find that things clearly perceived are most strongly fastened on our mind, and that such things as are proposed in order are more easily retained, then such as are confused.
How ever we shall yet further promote and help memory, if we get a tranquill and even spirit, and suffer not our understanding to be distracted about too many objects: and we shall the better retain things in memory if we oft go over them in our minds, diligently reflecting on them, and attending to them as we speak them.
Cap. 2. of Special method and first of Analysis.
The word Method is here to be taken somewhat more strictly then it was in the preceeding article: for our design there was only to teach Novists what order they ought to keep in the obtaining of knowledge: Whereas here we are not only to treat of the forming conceptions, but also enquiry is to be made how we may regularly dispose our conceptions when framed. and therefore
Method is 2 fold; for it either finds out the truth and so is called Analysis, or method of Resolution (which likewise may be termed method of invention) or it teaches the truth when found out, and is termed Synthesis, or method of composition, which likewise may be called the method of handling a doctrine.
Of Analysis
The whole body of any science is seldom Analysed or delivered Analytically; Analysis being only in use to solve questions. Every question is either concerning a name, or a thing.
By the question of a name here we understand not that which hunts for names whereby things may by signified, but that which searches for things signfied by names, of this kind are such as tend to the solving of (Ænigma’s or) Riddles; and such as do explain the obscure sense of A criptical Reader.
The question of A thing is 4 fold.
- 1. when we search for a cause from effects: Thus when we consider the Attractive power in a Load Stone and enquire into the cause of it.
- 2. the 2d kind is; when from causes we find out effects as when we consider of the wind’s blowing and the water’s flowing, and enquire into the benefit of the one or other; how they might prove useful and advantagious to us.
- 3. the third kind is; when from parts we are lead to a knowledge of an whole: thus many numbers being given, enquiry is made what the summe of all would be, they being added together.
- 4. the 4th and last kind is; when an whole being given and one part, enquiry is made what another part is. thus when a numberd is given, and part of it is taken away, we ask, what is the remainder.
Here we are to note that as in Analysis so in synthesis, we are evermore to proceed from A thing more known to a that which is less known, this rule is common to all method, neither is any method to be accounted good which at all deviates from this principle: yet in this, Analysis or method of Resolution differs from that which is called method of composition, that Analysis proceeds from lesse generalls to more generalls, whereas synthesis begins at a more general and goes to a less general: for thus if we enquire whether man’s soul is Immortal its evident that we do not go from universal axioms after this manner, nulla substantia propriè dess{…}itur, destructio nihil aliud est, quam partium dissollutio, and thence quod partibus caret destrui nequit;104 but on the other hand we gradually arise to those general notions: so that those 2 methods [Analysis and Synthesis] do not differ among themselves any other way than the ascent & descent of the same mountain: or the way whereby we go from a valley to the top of a mountain and that very way whereby we go from the top of the mountain to the valley which lies at the foot of it.105
Cap. 3. Of the Method of Composition.
Synthesis, or method of composition consists cheifly in this, that it proceeds from more general things to lesse generals and from more simple to more compounded things: and by this mode of proceeding all repetitions are avoided which ever more breed either confusion or tediousness.
That this method may be in all respects taught clearly, and first to obtain it’s designed end, Viz a clear and distinct knowledge of the truth, many things are heedfully to be observed: but since generall precepts separated from all matter are very difficult to be understood; we shall consider the synthesis of Geometricians which is always thought most efficacious to demonstrate truth and persuade: we shall therefore show what is commendable in their Method, & then propose what their defects and failings were.
Since then Geometricians design’d to assert nothing but was most evident and certain, they Imagined that this their design might be attained if so be that they did heedfully observe these 3 rules.
- 1. that they left nothing ambiguous in the terms proposed.
- 2. that they deduced reasoning only from certain and evident principles; such principles as could be doubted of by no man that had his witts about him.
- 3. that they demonstratively proved every conclusion: demonstratively. i.e. by the help of premised definitions, evident and granted axiomes, or propositions which no sooner are demonstrated but obtain the title of principles
To these 3 heads the whole of what Geometricians observe may be reduced, and so far they kept to a good rule and fam’d themselves, in that hereby they banished all disputations and controversies out of their schooles.
Nevertheless it cannot be denied, but that they have fallen into some errors or defects, which althô (possibly) they have not carried them from their proposed end, have led them thrô many by-wayes and occasioned much roughness, of which their method or way might have been void, and wholly destitute.
Their defects then were
- 1. That they laboured more about certainty then evidence; more about convincing the understanding then enlightning it. that is they laboured not so much to show the way how these and those truths came to be so, as to demonstrate that they are truths.
- 2. that they oftentimes prove those things which need no proof, i.e. althô they acknowledge that such things as are clear of themselves need no truth, yet they often attempt the proof of such truths.
- 3. that they demonstrate by something impossible, i.e. by some absurdity or Impossibility that would arise from that which is contrary to their Position:
- 4. that they demonstrate by things aliene & remote. This is an Imperfect way of demonstrating, being contrary to the ordinary course of nature which takes but one step at once.
- 5. that they do not observe the natural order of things i.e. by going from simples to compounds, and from generals to particulars: this fault, as also the 4th and some others are too often to be found in Euclids Elements.
- 6. that they do not sufficiently use divisions and partitions.
That which is censured and found fault with here as to the method of Geometricians is not, that they omitt any species of a genus which they design at any time to handle, but this viz—that they do not at first say of the genus that it has so many species and cannot have more because the general Idea of the genus cannot receive more differences and so proceed to the species: to make this more plain let us take this example.
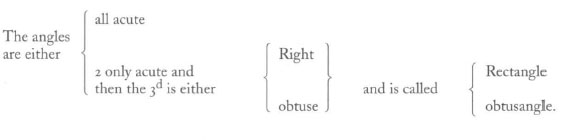
Euclid in his first book has definitions of all the species of a triangle without premising the distribution of triangle in general; now who can but see that it would be much more clear if the matter were thus proposed.
A Triangle may be divided either according to it’s sides or according to it’s angles,
Thus have we at Large shown what is good & what is bad in the method of Geometricians and hence: we may be abundantly informed as to method in general, or in other sciences when we are called to make use of it therein.
Cap. 4. of the 8 principle Rules relating to Method.
From what has been said in the foregoing chapter it may be Justly concluded that we shall attain to a method indeed more perfect and absolute than that which is in use among Geometricians themselves, if so be that we do carefully attend unto 8 rules which we shall here propose, whereof the 2 first do belong to Idea’s and so respect the first part of Logick; the next do belong to axiomes and consequently the 2d part: the 5 and 6th do respect argumentation and are related to the 3d part: and the 2 last rules are about order and so more Immediately belong to the fourth and last part of Logick.
The 2 Rules of definitions.
- 1. That we Leave nothing obscure, ambiguous or equivocal in the terms, but define the same most plainly.
- 2. That in all definitions we evermore use terms either perfectly known in themselves, or such as were before sufficiently explained.
The 2 Rules of axiomes
- 3. That we lay down no axiome (or nothing for an axiome) which is not amost clear and evident truth.
- 4. That we take that only for evident, which by a moderate attention is known to be a truth.
The 2 Rules of demonstration.
- 5. That we prove all obscure propositions, by the help of premised definitions being granted axiomes or demonstrated propositions.
- 6. That we never abuse the ambiguity of terms.
The 2 Rules of Method
- 7. That we handle things, as much as we can, according to natural order, by beginning at the more generals and the more simple, and by explaining whatever belongs to the nature of a genus before we descend to particular species.
- 8. That we divide as far as we can every genus into it’s species, every totum into all it’s parts and every difficulty into all it’s cases.
In those 2 last rules are inserted those words (as far as we can) for it somtimes happens that they cannot be rigorously observed, whether by reason of the limits of mans mind, or those bounds which we are forced to assign every science.
And thus we have proposed these 8 rules, which if we attend heedfully to, will be of great use to us in delivering any science, as the neglect and non-observance thereof will prove prejudicial unto knowledge and with these rules doth our fourth and last part of Logick conclude.
Upon the prickly bush of Logick grows
of other Sciences the fragrant rose.106
This book has been designed following, with some modifications, the Colonial Society of Massachusetts’ Volume 33, as designed and printed by D.B. Updike, Merrymount Press, Boston, in 1940, and also following the handwritten manuscripts, which were individually remarkably consistent and even elegant in their lay-out. The type is Adobe Caslon family, based on the font as originally designed by William Caslon in 1725. The binding is smythe sewn. All materials are library grade.
Editing, design, and production are by Elizabeth M. Burke of Portland, Maine. The dust jacket design is by Jeannie Abboud of West Acton, Massachusetts. Typesetting is by Pine Tree Composition, Lewiston, Maine; printing by BookCrafters at Fredericksburg, Virginia.
* All page citations of Charles Morton’s A Logick System and William Brattle’s Compendium of Logick refer to the editions transcribed in this volume.
1 Perry Miller, The New England Mind: The Seventeenth Century (Cambridge: Harvard, 1939), 69.
2 Charles Morton, Compendium Physicae, eds. Samuel Eliot Morison and Theodore Hornberger, Publications of the Colonial Society of Massachusetts, vol. 33 (Boston, 1940), 200.
3 Walter J. Ong, “Introduction” to A Fuller Course in the Art of Logic Conformed to the Method of Peter Ramus, 1672, ed. and trans. Walter J. Ong and Charles J. Ermatinger in The Complete Works of John Milton, vol. 8 (New Haven: Yale, 1982), 148.
4 Norman Fiering, “Rationalist Foundations of Jonathan Edwards’s Metaphysics” Jonathan Edwards and the American Experience, eds. Nathan O. Hatch and Harry S. Stout (New York, Oxford, 1988), 76.
5 The most informed examples of this are Norman Fiering’s “The First American Enlightenment: Tillotson, Leverett, and Philosophical Anglicanism,” The New England Quarterly 54 (1981): 307–344; and Daniel Walker Howe’s “The Cambridge Platonists of Old England and the Cambridge Platonists of New England,” Church History 57 (1988): 470–485. Howe writes “All in all, the Cambridge Platonists seem to have been better received by the American Puritans than they were by their English contemporaries” (pp. 472–73).
6 See Howe, “The Cambridge Platonists,” 472–73.
7 John Tillotson, The Rule of Faith of an Answer to the Treatise of Mr. I.S. entitled Sure-footing, etc, 2nd ed. (London: 1676), 5.
8 John Spurr, “‘Latitudinarianism’ and the Restoration Church,” The Historical Journal 31 (1988): 66, see also p. 73 for Tillotson.
9 Thomas Goddard Wright, Literary Culture in Early New England 1620–1730 (New Haven: Yale, 1920), 265–272.
10 A Catalogue of Curious and Valuable Books belonging to the late Reverend and Learned Ebenezer Pemberton (Boston, 1717).
11 Benjamin Franklin, Writings, ed. J.A. Leo Lemay (New York: Library of America, 1987), 1321 and 337–38; and Poor Richard’s Books: An Exhibition of Books Owned by Benjamin Franklin, comp. James Green (Philadelphia: Library Company of Philadelphia, 1990), 18.
12 See Norman Fiering, Jonathan Edwards’s Moral Thought and Its British Context (Williamsburg: Institute of Early American Culture, and Chapel Hill: University of North Carolina, 1981), 28–48. William Sparkes Morris, The Young Jonathan Edwards: A Reconstruction (Brooklyn: Carlson, 1991), 80–82. Edwards was also told to procure and read The Port-Royal Logic for his Yale education.
13 Charles E. Hambrick-Stowe, The Practice of Piety: Puritan Devotional Disciplines in Seventeenth-Century New England (Williamsburg: Institute of Early American History and Culture, and Chapel Hill: University of North Carolina, 1982). Related is the possible influence of Ignatius Loyola’s Spiritual Excercises on Descartes’s Meditations. Bradley Rubidge reviews the literature on this influence in “Descartes’s Meditations and Devotional Meditations,” Journal of the History of Ideas 51 (1990): 27–49.
14 John Morgan, Godly Learning: Puritan Attitudes towards Reason, Learning, and Education, 1550–1640 (Cambridge: Cambridge, 1986), 232. Another similar study of the dynamics of the classroom, and specifically with Ramist logic is Anthony Grafton and Lisa Jardine, From Humanism to Humanities: Education and the Liberal Arts in Fifteenth and Sixteenth-Century Europe (Cambridge: Harvard, 1986). Cartesianism in the classroom is discussed in Michael Heyd, Between Orthodoxy and the Enlightenment: Jean-Robert Chouet and the Introduction of Cartesian Science in the Academy of Geneva (Boston: M. Nijhoff, 1982); and Martin Klauber, “Reason, Revelation, and Cartesianism: Louis Tronchin and Enlightened Orthodoxy in Late Seventeenth-Century Geneva,” Church History 59 (1990): 326–339. See also Michael Shank, Unless You Believe, You Shall Not Understand: Logic, University, and Society in Late Medieval Vienna (Princeton: Princeton, 1988); and L.W.B. Brockliss, French Higher Education in the Seventeenth and Eighteenth Centuries: A Cultural History (Oxford: Clarendon, 1987).
15 C.A.J Coady, Testimony: A Philosophical Study (Oxford: Clarendon, 1992); Steven Shapin, A Social History of Truth: Civility and Science in Seventeenth-century England (Chicago: University of Chicago, 1994); and John Hardwig, “The Role of Trust in Knowledge,” Journal of Philosophy 88 (1991): 693–708.
16 Historical interpretations of the humanists’ transformation of logic fall into three groups: 1) Those who disparage the logic for its degradation of formal syllogistic logic such as William and Martha Kneale, The Development of Logic (Oxford: Clarendon, 1962); 2) those who emphasize the continuation of Medieval aspects in the new logic such as E.J. Ashworth in Language and Logic in the Post-Medieval Period (Boston: Reidel, 1974), and Charles B. Schrmitt, John Case and Aristotelianism in Renaissance England (Montreal: McGill-Queen’s, 1983); and 3) those who emphasize its sources in Classical rhetoric and new achievements in theories of method such as Wilbur Samuel Howell, Logic and Rhetoric in England, 1500–1700 (Princeton: Princeton, 1956); Walter Ong, Ramus, Method, and the Decay of Dialogue (Cambridge: Harvard, 1958); and Lisa Jardine in “Lorenzo Valla and the Intellectual Origins of Humanistic Dialectic,” Journal of the History of Philosophy 15 (1977): 143–164, and “Humanism and the Teaching of Logic,” The Cambridge History of Later Medieval Philosophy, eds. Norman Kretzman, Anthony Kenney, and Jan Pinborg (Cambridge: Cambridge, 1982), 797–807. My introduction fits in the third category. See also E.J. Ashworth, The Tradition of Medieval Logic and Speculative Grammar from Anselm to the End of the Seventeenth Century: A Bibliography from 1836 Onwards (Toronto: Pontifical institute of Mediaeval Studies, 1978).
17 See Jardine, “Lorenzo Valla and the Intellectual Origins of Humanistic Dialectic.”
18 Ramus is quoted, in translation, in Lisa Jardine, “Distinctive Discipline: Rudolph Agricola’s Influence on Methodical Thinking in the Humanities,” Rudolphus Agricola Phrisius 1444–1485: Proceedings of the International Conference at the University of Groningen, 28–30 October, 1985, eds. F. Akkerman and A.J. Vanderjagt (Leiden: E.J. Brill, 1988), 39.
19 See Clyde Leonard Manschreck, Melanchthon: The Quiet Reformer (New York: Abingdon Press, 1958); John R. Schneider, Philip Melanchthon’s Rhetorical Construal of Biblical Authority: Oratio Sacra (Lewiston, N.Y.: The Edwin Mellen Press, 1990); and E.J. Ashworth, Language and Logic in the Post-Medieval Period, 13–14.
20 Translated in Schneider, Philip Melanchthon’s Rhetorical Construal of Biblical Authority, 16. See Melanchthon’s declamation, Vita Rodolphi Agricolae, in Corpus Reformatorum: Philippi Melanthonis Opera Quae Supersunt Omnia, vol. 11, ed. Carolus Gottlieb Bretschneider (New York: Johnson Reprint, 1963), 438–446.
21 Translated in Schneider, Philip Melanchthon’s Rhetorical Construal of Biblical Authority, 16. See Melanchthon’s declamation, Vita Rodolphi Agricolae, in Corpus Reformatorum: Philippi Melanthonis Opera Quae Supersunt Omnia, vol. 11, ed. Carolus Gottlieb Bretschneider (New York: Johnson Reprint, 1963), 438–446.
22 Full tides and lists of each textbook’s editions are given at the beginning of the Erotemata Dialectices in Corpus Reformatorum, vol. 13, 508–510.
23 See Jardine, “Lorenzo Valla and the Intellectual Origins of Humanistic Dialect,” 147.
24 Rudolphus Agricola, De lnventione Dialectica Libri Tres (Argentinae, 1521), Bk. 1, chap. 24, p. 36. The modern facsimile of a 1539 edition of Agricola’s text (Nieuwkoop, 1967) is substantially different from the 1521 edition available on microfilm. The section on testimony and faith in the 1539 text does not include a discussion of divine testimony.
25 Melanchthon, Erotemata Dialectices in Corpus Reformatorum, vol. 13, 707–711.
26 Bartolomaeus Keckermann, Gymnasium Logicum id est De Usu & Exercitatione Logicae Artis Absolutoiri & pleniori, Liberi Tres (London, 1606), 27–29.
27 Augustine, On Christian Doctrine, Bk. 2, chap. 11, sect. 60, trans. J.F. Shaw, in A Select Library of the Nicene and Post-Nicene Fathers of the Christian Church, ser. 1, vol. 2, ed. Philip Schaff (Grand Rapids: Wm. B. Eerdmans, 1988), 554.
28 Augustine gives women a lesser position than men in the natural order, but adamantly states “so that the image of God may remain on that side of the mind of man which cleaves to the beholding or the consulting of the eternal reason of things; and this, it is clear, not men only, but also women have” (On the Trinity, Bk. 12, chap, vii, trans. Arthur West Haddan in A Select Library of the Nicene and Post-Nicene Fathers of the Christian Church, Ser. 1, vol. 3, 158–159). Charles Morton’s “Preface to the Reader,” in A Logick System, justifies his use of English by declaring his compassion for those of either sex who could use logic but have not had the opportunity to learn Latin (p. 141). Brattle’s use of the vernacular probably indicates a similar concern.
29 Augustine, On the Trinity, Bk. 12, chap. 11. Trans. Haddan, Ser. 1, vol. 3, 160.
30 Quoted in Lisa Jardine, “Humanism and the Teaching of Logic,” 801.
31 Cited as “Melanchj Logica” in the appendix of Thomas Wright’s Literary Culture in New England 1620–1730 (New Haven: Yale, 1920), 269. Agricola’s logic also does not appear in Harvard’s 1723 library catalog.
32 The most recent work on Ramism, covering the life and influence of Ramus on logic and rhetoric from the Renaissance through the nineteenth century in England and America, is Richard E. Dickson’s, Ramism and the Rhetorical Tradition (Ph.D. dissertation, Duke University, 1992). I benefitted greatly from discussions with Professor Dickson.
33 Peter Ramus, The Logike of the Most Excellent Philosopher, P. Ramus, Martyr, trans. Roland MacIlmaine, ed. Catherine M. Dunn (Northridge: San Fernando State College, 1969, transcription of 1574 edition), 6.
34 On Ramus and Ramist reforms, see Walter J. Ong, Ramus: Method, and the Decay of Dialogue (Cambridge, Mass.: Harvard University Press, 1958), and Grafton and Jardine, From Humanism to Humanities. On English Ramists, see Howell, Logic and Rhetoric in England, 1500–1700.
35 The Logicke of the Moste Excellent Philosopher, P. Ramus, Martyr, 5.
36 The Logicke of the Moste Excellent Philosopher P. Ramus, Martyr, 37.
37 Sixteenth-century Ramist logics at Cambridge include William Temple’s 1584 Latin edition of Ramus with a commentary, and Friedrich Beurhaus’s three Ramist textbooks, one titled Triumphus Logicae Ramae (1589). Ramism especially influenced Puritanism at Christ’s College in the classes and tutorials of Laurence Chaderton (c. 1536–1604), William Perkins (1558–1602), and George Downame (d. 1634).
38 See Keith L. Sprunger, The Learned Doctor William Ames: Dutch Backgrounds of English and American Puritanism (Urbana: University of Pennsylvania, 1979); and the translation of the Medulla as The Marrow of Theology, trans. John Dykstra Eusden (Durham: Labyrinth, 1983).
39 Miller, The New England Mind: The Seventeenth Century, 500. Miller’s appendix, “The Literature of Ramus’ Logic in Europe,” (pp. 493–501) is excellent.
40 For the most recent work on Richardson, see John C. Adams, “Alexander Richardson’s Puritan Theory of Discourse,” Rhetorica 4 (1986): 255–274; “Alexander Richardson’s Philosophy of Art and the Sources of the Puritan Social Ethic,” Journal of the History of Ideas 50 (1989): 227–247; “Ramus, Illustrations, and the Puritan Movement,” Journal of Medieval and Renaissance Studies 17 (1987): 195–210.
41 Alexander Richardson, The Logicans School-Master: or, A Comment Upon Ramus Logicke (Cambridge: 1629), 18.
42 Richardson, The Logicians School-Master, 19.
43 Richardson, The Logicians School-Master, 78.
44 Richardson, The Logicians School-Master, 60–63 and 222–235.
45 Richardson, The Logicians School-Master, 223.
46 See Coady, Testimony: A Philosophical Study; Steven Shapin, A Social History of Truth; and Barbara Shapiro, “Beyond Reasonable Doubt” and “Probable Cause”: Historical Perspectives on the Anglo-American Law of Evidence (Berkeley: University of California, 1991).
47 Richardson, The Logicians School-Master, 61.
48 Richardson, The Logicians School-Master, 222–223.
49 Richardson, The Logicians School-Master, 63.
50 Richardson, The Logicians School-Master, 63.
51 Thomas Spencer, The Art of Logick, ed. R.C. Alston (Menston: Scolar, 1970), 38.
52 Richardson, The Logicians School-Master, 226–27.
53 Richardson, The Logicians School-Master, 227.
54 Gerhard Reedy, The Bible and Reason: Anglicans and Scripture in Late Seventeenth-Century England (Philadelphia: University of Pennsylvania, 1985), 57–58.
55 See the entry on Keckermann in the Dictionary of Scientific Biography, vol. 7, ed Charles Coulston Gillispie, (New York: Charles Scribner’s Sons, 1973), and the section devoted to Keckermann in Neal W. Gilbert, Renaissance Concepts of Method (New York: Columbia University, 1960), 214–220. I use the London edition of Keckermann’s logic, titled Gymnasium Logicum id est De Usu & Exercitatione Logicae Artis absolutoiori & pleniori, Liberi Tres (1606). Keckermann also wrote an influential critique of logic, Præcognitorum Logicorum Tractatus Tres (Hanover, 1604). Keckermann’s logic is put in its Continental context in Ashworth’s introduction to Language and Logic in the Post-Medieval Period.
56 Walter Ong discusses some Medieval devices in Ramus, Method, and the Decay of Dialogue, 74–91; and E.J. Ashworth offers technical explanations of “Barbara Celerant” and the AEIO in “Some Notes on Syllogistic in the Sixteenth and Seventeenth Centuries,” Notre Dame Journal of Formal Logic 11 (1970): 17–33.
57 Keckermann, Gymnasium Logicum, 83.
58 Keckermann, Gymnasium Logicum, 84–85.
59 Keckermann, Gymnasium Logicum, 169.
60 See Schmitt, John Case and Aristotelianism in Renaissance England.
61 Neal Gilbert in Renaissance Concepts of Method, 167–170, discusses Zabarella’s sources.
62 Jacobi Zabarella, Opera Logica (Hildesheim: Georg Olms Verlagsbuchhandlung, 1966, reprint of 1597 edition), 100–101.
63 My statement is based on an edition published in London in 1662. William Morris in The Young Jonathan Edwards, 79–80, notes that Edwards at Yale used a 1660 edition of Heereboord’s logic that was bound with a 1651 edition of Burgersdijck’s. This would have served to Christianize Burgersdijck. Morris analyzes Heereboord and Burgersdijck pp. 80–102. Heereboord’s influence at Harvard was primarily through his Meletemata Philosophica (1654); see Samuel E. Morison in Harvard in the Seventeenth Century, vol. 1 (Cambridge, MA.: Harvard University, 1936), 233–234.
64 See Schmitt, John Case and Aristotelianism in Renaissance England, and E.J. Ashworth’s introduction to Sanderson’s Logicae Artis Compendium, ed. and intro. E.J. Ashworth (Bologna: Cooperativa Libraria, 1985).
65 See Ashworth’s introduction to Robert Sanderson, Logicae Artis Compendium.
66 The translation is by Samuel Howell in Logic and Rhetoric in England, 1500–1700, 303.
67 Zachary Coke, The Art of Logick, (Menston, Eng: Scholars Press, 1969; reprint of 1654 edition), third page of “Epistle Dedicatory.”
68 Coke, The Art of Logick, fifth page of “Episde Dedicatory.”
69 Coke, The Art of Logick, eleventh page of “Epistle Dedicatory.”
70 Coke, The Art of Logick, fifteenth page of “Epistle Dedicatory.”
71 The advertisement is partially quoted in the second edition’s Online Computer Library Center (OCLC) citation. The only cited copy of the book is owned by the William Andrews Clark library where a librarian read to me the whole quote over the phone. John Goodin, librarian at Indiana University Southeast, showed me this crucial information.
72 For Roger Williams on Ainsworth, see Ainsworth’s entry in the Dictionary of National Biography.
73 Quoted in Cotton Mather, “An Account of the University,” Magnalia Christi Americana (London, 1702), Bk. 4, Introduction, pt. 2. sect. 7; translation by Lucius F. Robinson in the 1852 edition, reprinted 1967 by Russell & Russell.
74 Quoted in Thomas J. Siegel, Governance and Curriculum at Harvard College in the 18th Century (Ph.D. dissertation, Harvard University, 1990), 383.
75 See Harold Love, Scribal Publications in Seventeenth-century England (Oxford: Clarendon, 1993). For various assessments of Renaissance textbooks, see Neal Gilbert, Renaissance Concepts of Method, 71–73, and Anthony Grafton, “Teacher, Text and Pupil in the Renaissance Classroom: A Case Study from a Parisian College,” History of Universities 1 (1981): 37–70, and Anthony Grafton and Lisa Jardine, From Humanism to Humanities.
76 Cotton Mather’s sketch of Eliot is reprinted in The Puritans, vol. 2, ed. Perry Miller and Thomas H. Johnson (New York: Harper Torchbooks, 1963), 497–511. James Axtell puts Eliot in the context of European work in education among American Indians in The Invasion Within: The Contest of Cultures in Colonial North America (New York: Oxford, 1985); see especially the discussion of Eliot’s textbooks on pp. 223–25.
77 Eliot, A Logick Primer, (Cambridge, 1672), title page.
78 Antoine Arnauld, The Art of Thinking: Port-Royal Logic, “First Discourse,” trans. James Dickoff and Patricia James (Indianapolis: Bobbs-Merrill, 1964), 15. Citations of page numbers in subsequent footnotes are from this translation.
79 Dugald Stewart, “A General View of the Progress of Metaphysical, Ethical, and Political Philosophy Since the Revival of Letters in Europe,” in Dissertations on the Progress of Knowledge (NY: Arno Press, 1975), 74.
80 See “A Declamation on the Subject of Early Liberal Education for Children,” trans. Beert C. Verstraete, Collected Works of Erasmus, vol. 26, ed. J.K. Sowards (Toronto, University of Toronto, 1985).
81 John Milton, “Prolusions,” Complete Poems and Major Prose, ed. Merritt Y. Hughes (Indianapolis: Odyssey, 1957), 627; see also Milton’s criticisms of logic in “Of Education,” 636.
82 See The Educational Writings of John Locke, ed. James Axtell (Cambridge: Cambridge, 1968), and W. Henry Kenney, John Locke and the Oxford Training in Logic and Metaphysics (Ph.D. dissertation, Saint Louis University, 1959).
83 Cotton Mather, Manductio ad Minsterium: Directions for A Young Candidate of the Ministry (Boston, 1726), 35–36.
84 Cotton Mather, Manductio ad Minsterium, 35–36.
85 In the 1683 and subsequent editions, Arnauld even expanded the religious direction of the text because of “theological disputes.” See “Preface to Fifth Edition.”
86 Richard H. Popkin, The History of Scepticism from Erasmus to Spinoza (Berkeley: University of California, 1979).
87 Quoted in Richard Southern, Saint Anselm: A Portrait in a Landscape (Cambridge: Cambridge, 1990), 51.
88 Blaise Pascal, Pensées, # 131, trans. A. J. Krailsheimer (New York: Penguin Books, 1966), 63–64.
89 Michel de Montaigne, An Apology for Raymond Sebond, trans. M.A. Screech (London: Penguin, 1987), 13.
90 Montaigne, An Apology for Raymond Sebond, trans. M.A. Screech (New York: Penguin, 1987), 67–68.
91 Pascal, Pensées, #680, #780: 243, 263.
92 Arnauld, The Art of Thinking: Port-Royal Logic, Bk. 3, chap. 20, sect. 6, 271–273.
93 René Descartes, The Philosophical Writings of Descartes, vol. 1, trans. John Cottingham, Robert Stoothoff, Dugald Murdoch (Cambridge: Cambridge, 1985), 113.
94 Descartes, Philosophical Writings, vol. 1, 119.
95 Descartes, Philosophical Writings, vol. 1, 125.
96 Letter to Mersenne, 15 April 1630, quoted in E.M. Curley, Descartes Against the Skeptics (Cambridge: Harvard, 1978), 13n.
97 Descartes, Philosophical Writings, vol. 2, 35.
98 Popkin, The History of Scepticism from Erasmus to Spinoza, 191. See also, Edward Downey, The Knowledge of God in Calvin’s Theology (New York, 1952), and Dewey Hoitenga, “Faith and Reason in Calvin’s Doctrine of Knowledge,” in Rationality in the Calvinian Tradition, eds. Hendrik Hart, Johan Van der Hoeven, Nicholas Wolterstorff (Lanham: University Press of America, 1983), 17–42.
99 Bernard Williams, Descartes: The Project of Pure Enquiry (Atlantic Highlands: Humanitities, 1978), 16. For an intriquing interpretation of the role of these dreams in Descartes’s work, see Gregor Sebba, The Dream of Descartes, ed. Richard A. Watson (Carbondale: Southern Illinois University, 1987).
100 Quoted in Williams, Descartes: The Project of Pure Enquiry, 32.
101 Descartes, Philosophical Writings, vol. 2, 150.
102 Descartes, Philosophical Writings, vol. 2, 154.
103 See Stephen R.L. Clark, “Descartes’ Debt to Augustine,” Philosophy, Religion, and the Spiritual Life, ed. Michael McGhee, (Cambridge: Cambridge, 1992), 73–88.
104 Arnauld wrote two letters to Descartes in 1648 expressing his satisfaction with Descartes’s responses. These letters and his minor objections are analyzed in Steven Nadler, Arnauld and the Cartesian Philosophy of Ideas (Manchester: Manchester University, 1989), 24.
105 Richard Watson, The Breakdown of Cartesian Metaphysics (Atlantic Highlands: Humanities, 1987), 21.
106 On Descartes’s hopes for his Principles, see Williams, Descartes: The Project of Pure Enquiry, 21–22.
107 Kneale, The Development of Logic, 321.
108 Wilbur Samuel Howell, Eighteenth-Century British Logic and Rhetoric (Princeton: Princeton, 1971), 299–371.
109 Arnauld, The Art of Thinking: Port-Royal Logic, “Preface to fifth edition,” 5. Dickoff’s and James’s translation is rather loose and has been criticized by those concerned that it might lead to misunderstandings about terms and their context that a more literal translation would avoid. (See Richard Watson, “The Port-Royal Logic in the Twentieth Century,” journal of the History of Philosophy 5 (1967): 55–60; and Roland Hall’s review of The Art of Thinking in The Philosophical Quarterly 16 (1966): 75–76.) For the purposes of my book, which avoids precise discussion of terms, the translation is the most easily accessible and serves to express the vigor of Arnauld’s thought without confusing the essential structure of the book. I confess that my own language skills do not include the ability to work from the originial French text, but I have endeavored to check my quotes with both seventeenth-century Latin editions and L’Art de Penser: La Logique de Port-Royal, 3 vols. eds. Bruno Baron von Freytag Loringhoff and Hervert E. Brekle (Stuttgart-Bad Cannstatt, Friedrich Frommann Verlag, 1967).
110 For the synod’s influence on Jansen, see Alexander Sedgwick, Jansenism in Seventeenth-Century France (Charlottesville: Virginia, 1979), 48.
111 The term “Augustinian strain of piety” comes from Perry Miller’s analysis of Puritanism in The New England Mind: The Seventeenth Century, 3–34.
112 For an overview of the whole Jansenist movement, see Sedgwick, Jansenism in Seventeenth-Century France. For a more spirited Roman Catholic perspective which puts Jansenism in the context of other French reform movements, see H. Daniel-Rops, The Church in the Seventeenth Century, trans. J. J. Buckingham (New York: E. P. Dutton, 1963), 327–425.
113 Sedgwick, Jansenism in Seventeenth-Century France, 34.
114 H. Daniel-Rops, The Church in the Seventeenth Century, 362.
115 On the life and thought of Arnauld, see Steven M. Nadler, Arnauld and the Cartesian philosophy of Ideas; “Arnauld, Descartes, and Transubstantiation: Reconciling Cartesian Metaphysics and Real Presence,” Journal of the History of Ideas 49 (1988): 229–246; R. C. Sleigh, Leibniz and Arnauld: A Commentary on Their Correspondence (New Haven, Yale University, 1990); and John Kilcullen, Arnauld, Bayle, and Toleration (Oxford: Clarendon, 1988).
116 The Port-Royal Logic was initially published anonymously. Pierre Nicole is usually cited as the co-author, and he certainly had something to do with its authorship; however, the text closely follows Arnauld’s thought, and I follow James Dickoff and Patricia James in citing only Arnauld as the author. Alexander Sedgwick believes that Pascal was “very likely” one of the authors (p. 97) since it was written during the period that the Pensées was being written. Arnauld and Pascal shared much in common; however, it seems unlikely that Pascal was an author any more than others in the Port-Royal circle who might have offered suggestions as the manuscript circulated. See Rick Kennedy, “The Application of Mathematics to Christian Apologetics in Pascal’s Pensées and Arnauld’s The Port-Royal Logic” Fides et Historia 23 (1991): 37–52.
117 Howard C. Barnard, The Port-Royalists on Education: Extracts from the Educational Writings of the Port-Royalists (Cambridge: Cambridge, 1918), 22. See also H. C. Barnard, The Little Schools of Port-Royal (Cambridge: Cambridge, 1913).
118 As an example of their innovative methods, a card game was invented for the students in which “imperial and papal lines took the place of the usual suits. Each card bore the name and history of a particular emperor or pope. A game of two-handed whist was concocted whereby the longer reign took the trick and the loser repeated from memory the details on the card” (L. W. B. Brockliss, French Higher Education in the Seventeenth and Eighteenth Centuries, 90). The importance they placed on education is shown by one of their dictums: “Nothing is more detestable” than people who treat a tutor like a “hireling.” (Barnard, The Port-Royalists on Education, 99). See also Robert Lang, “Rhetoric Les Petites-Ecoles of Port-Royal,” Communication Monographs 25 (1958): 208–214; Jan Meil, “Pascal, Port-Royal, and Cartesian Linguistics,” Journal of the History of Ideas 30 (1969): 261–271; and Steven Nadler, “Cartesianism and Port-Royal,” Monist 71 (1988): 573–584. Nadler shows that few of the solitaires were committed to Cartesian philosophy as a whole. The schools cannot be considered disseminators of an integrated Cartesian philosophy.
119 Antoine Arnauld and Claude Lancelot, Grammaire Generate et Raisonnee (1660). The quote in the text is from an excerpt in Barnard, The Port-Royalists on Education, 142.
120 Arnauld, The Art of Thinking: Port-Royal Logic, “Foreword,” 4.
121 Aside from the Discourse and Principles, Arnauld relied heavily on Descartes’s Rules for the Direction of the Mind (Descartes, Philosophical Writings, vol 1: 7–78) which was unpublished at the time but passed through Arnauld’s hands in manuscript during the 1650s.
122 Arnauld, The Art of Thinking: Port-Royal Logic, “First Discourse,” 12–13.
123 Arnaud, The Art of Thinking: Port-Royal Logic, “Second Discourse [1664],” 25–26.
124 Arnauld, The Art of Thinking: Port-Royal Logic, “Second Discourse [1664],” 21.
125 Ong, “Introduction,” Complete Works of John Milton, 165–166.
126 Sprunger, The Learned Doctor William Ames, 117
127 Arnauld, The Art of Thinking: Port-Royal Logic, Bk. 4, chap. 7, 323–325.
128 Arnauld, The Art of Thinking: Port-Royal Logic, Bk. 4, chap. 7, 324–325.
129 Arnauld, The Art of Thinking: Port-Royal Logic, Bk. 3, chap. 20, sect. 6, 286. “Faulty Arguments Arising from the Objects Themselves,” Bk. 3, chap. 20, sect. 6, 286; see also Bk. 4, chap. 12, 338–339.
130 Arnauld, The Art of Thinking: The Port-Royal Logic, “Faulty Arguments Arising from the Objects Themselves,” Bk. 3, chap. 20, sect. 6, 286–287.
131 There is no comprehensive study of The Port-Royal Logic’s influence; however, preliminary information is available in Brockliss, French Higher Education, 197–204; Howell, Logic and Rhetoric in England, 1500–1700, 342–363, Charles W. Hendel, “Foreword” in Dickoff’s and James’s edition of The Art of Thinking, xvii–xxv, and Richard Watson, “The Port-Royal Logic in the Twentieth Century,” Journal of the History of Philosophy 5 (1967): 55–60.
132 These numbers come from the list of editons and translations in L’Art de Penser, vol. 2, ed. Loringhoff and Brekle, 19–23. As for the editions in England, there is a distinctive break between the eight published before 1717 and the four published after 1818. This break might indicate a general abandonment of Cartesian logic, but we must keep in mind the influence of The Port-Royal Logic on logics that were popular in the eighteenth century.
133 Anthony LeGrand, An Entire Body of Philosophy, trans. R. Blome (London, 1694). All English quotations of the Institutio will be from Blome’s translation; however, I will also cite the book, chapter, and subheadings of the 1680 Latin edition. Blome states in his subtitle that his edition included “large additions of the author, never yet published.” At least in the logic section, there were no “large additions” although there are a few minor changes.
134 For LeGrand, see John K. Ryan “Anthony Legrand 1629–99: Franciscan and Cartesian,” New Scholasticism 9 (1935), 226–250; 10 (1936), 39–55, and the Dictionary of National Biography. For the most extensive study of LeGrand in the context of Cartesianism see Richard Watson’s “Introduction,” to Antoine LeGrand, An Entire Body of Philosophy (New York, Johnson Reprint Corporation, 1972), v–xi, and The Breakdown of Cartesian Metaphysics, 93–96.
135 LeGrand, Entire Body of Philosophy, trans. Blome, “The Preface” sect. 2.
136 Sterling Lamprecht, “The Role of Descartes in Seventeenth-century England,” Studies in the History of Ideas 3 (1935): 187.
137 John Hall, An Humble Motion to the Parliament of England concerning the Advancement of Learning and the Reformation of the Universities (London, 1649), 26; see also Marjorie Nicholson, “Early Stages of Cartesianism in England,” Studies in Philology 26 (1929): 361, and Lamprecht, “The Role of Descartes in Seventeenth-century England,” 195.
138 Henry More, Immortality of the Soul, ed. A. Jacob (Boston: Matinus Nijhoff, 1987), “Preface,” sect. 15, p. 20. Henry More’s relationship with Cartesianism has been often studied, especially for his vehement rejection of it after an initial embrace. More rejected only aspects of Cartesianism and never abandoned those aspects of Cartesian logic that followed Platonic lines, such as Descartes’s proof of the existence of God from an idea in the human mind.
139 Lamprecht, “The Role of Descartes in Seventeenth-century England,” 199, 195.
140 Quoted in Mark Curtis, Oxford and Cambridge in Transition, 1558–1642 (Oxford: Clarendon, 1959), 257–58.
141 Anthony Wood, Athena Oxonienses, vol. 2 (London, 1692), 620.
142 J. W. Ashley Smith, “Appendix A,” The Birth of Modern Education: The Contribution of the Dissenting Academies 1660–1800 (London: Independent Press, 1954), 269–286.
143 Ashley Smith, The Birth of Modern Education, 274.
144 See Sergeant and Aldrich in the Dictionary of National Biography. Wilbur S. Howell’s Eighteenth Century British Logic and Rhetoric discusses both men’s logics. For Aldrich there is also a privately printed biography by W. G. Hiscock, Aldrich of Christ Church 1648–1710 (Oxford, 1960).
145 John Sergeant, The Method of Science, (London, 1696), “Preface Dedicatory,” n.p.
146 Leibniz quoted in Barnard Williams’s Descartes: The Project of Pure Enquiry, 32; Sergeant, The Method of Science, “Preface Dedicatory,” n.p.
147 Lamprecht, “The Role of Descartes in Seventeenth-century England,” 213–214; see these characterizations in a more drawn out form in John Sergeant, Solid Philosophy Asserted, (London, 1697), “Preface,” n.p.
148 This paragraph is translated by Howell in Eighteenth Century Logic and Rhetoric, 55
149 See Beverley C. Southgate, “‘Cauterising Tumour of Pyrrhonism’: Blackloism Versus Skepticism,” Journal of the History of Ideas 53, (1992): 631–645. Southgate, whose “Covetous of Truth”: The Life and Work of Thomas White, 1593–1676, will be published in 1996, wrote to me that she knows of no connection between LeGrand and the Blackloists.
150 For Digby and White, see their entries in the Dictionary of National Biography; for their interest in Descartes, see Lamprecht, “The Role of Descartes in Seventeenth-century England,” 189–195.
151 John of Salisbury offers an excellent history and analysis of the importance of categories in The Metalogicon, trans. Daniel D. McGarry (Gloucester, MA.: Peter Smith, 1971), 155–165.
152 See Southgate, “Blackloism Versus Scepticism,” 637.
153 Fiering, Moral Philosophy at Seventeenth-Century Harvard, 207.
154 Samuel Sewall, The Diary of Samuel Sewall, vol. 1, ed. M. Halsey Thomas (New York: Farrar, Straus and Giroux, 1973), 391.
155 Sewall, The Diary of Samuel Sewall, vol. 1, 391.
156 Edward Calamy, A Continuation of the Account of the Ministers, Lecturers, Masters, and Fellows of Colleges, and School-masters who were Ejected and Silenced after the Restoration in 1660 (London, 1627), 197.
157 The best biography of Morton is Samuel Eliot Morison’s introduction to volume 33 of the Publications of the Colonial Society of Massachusetts, which transcribed the Compendium Physicae (hereinafter cited as Morison, “Charles Morton”). Morison’s first footnote gives a bibliography of sources, to which should be added J. W. Ashley Smith’s discussion of Morton and his curriculum in The Birth of Modern Education: The Contribution of the Dissenting Academies 1660–1800, 56–61, and Norman Fiering’s chapter on Morton in Moral Philosophy at Seventeenth-Century Harvard, 207–238.
158 See Barbara Shapiro, John Wilkins, 1614–1672: An Intellectual Biography (Berkeley: University of California, 1969). See also the discussion of the intellectual life at Cambridge and Oxford during the late 1640s to 1660 in Mordechai Feingold’s “Isaac Barrow: Divine, Scholar, Mathematician,” and John Gasciogne “Isaac Barrow’s Academic Milieu: Interregnum and Restoration Cambridge” in Before Newton: The Life and Times of Isaac Barrow, ed. Mordechai Feingold (Cambridge: Cambridge University, 1990), 22–37, 250–290. Peter Lake’s Moderate Puritans and the Elizabethan Church (Cambridge: Cambridge, 1982) deals with an earlier period but is a standard introduction to various types of mentalities within Puritanism.
159 Calamy, A Continuation of the Account, 19–93.
160 See Michael R. Watts, The Dissenters (Oxford: Clarendon, 1978), and Herbert McLachlan, English Education Under the Test Acts: Being the History of the Non-Conformist Academies 1662–1820, (Manchester: Manchester University, 1931).
161 J. L. Tayler’s A Little Corner of London (Newington Green) with its History and Tradition of a Non-Conformist Meeting House (London, 1925), has a chapter on “The Morton Period and Its Struggle for Personal Freedom,” in which pp. 20–29 deal with Morton.
162 For these men and schools see McLachlan, English Education under the Test Acts; Smith, Birth of Modern Education; the Dictionary of National Biography, and Theodore Hornberger, “Samuel Lee (1625–1691), A Clerical Channel for the Flow of Ideas to Seventeenth-Century New England,” Osiris 1 (1936): 341–355.
163 Cotton Mather, “An Account of the University,” Magnalia Christi Americana, Bk. 4, Introduction, pt. 3, sect. 3.
164 Fiering, Moral Philosophy at Seventeenth-Century Harvard, 279–294.
165 Calamy, A Continuation of the Account, 211.
166 Fiering, Moral Philosophy at Seventeenth-Century Harvard, 281.
167 Tutor Henry Flint makes this count; see Morison, Harvard in the Seventeenth Century, vol. 1, 290–91.
168 Samuel Wesley, A Letter from a Country Divine to His Friend in London Concerning the Education of Dissenters in their Private Academies, 2nd ed. (London, 1704), 6.
169 Wesley, A Letter, 5.
170 Wesley, A Letter, 6.
171 Quoted in Smith, Birth of Modern Education, 58.
172 See Barnard, The Port-Royalists on Education.
173 Arthur O. Norton, “Harvard Text-Books and Reference Books of the Seventeenth Century,” Transactions, Colonial Society of Massachusetts 28 (1935), 421. Norton only cites Morton’s logic and physics textbooks.
174 Calamy, A Continuation of the Account, 197. Samuel Wesley in A Letter cited mathematics as Morton’s “chiefest excellence” (p. 5), but there is no mathematics in any of the extant textbooks.
175 Fiering, Moral Philosophy at Seventeenth-Century Harvard, 211–227, analyzes these three works and shows their context. The texts appear in the student notebook of Ebenezer Williams, the transcriptions done in February 1708.
176 Fiering, Moral Philosophy at Seventeenth-Century Harvard, 17, and “President Samuel Johnson and the Circle of Knowledge,” William and Mary Quarterly, 3rd series, 28 (1971): 199–236.
177 Morton, A Logick System, 238 of typescript.
178 The most popular Dutch encyclopedist among seventeenth-century Puritans was Johann Heinrich Alsted (1588–1638); see Morison, Harvard in the Seventeenth Century, vol. 1, 157–159.
179 See Cotton Mather’s speculation on this that cites a conversation with Morton in Selected Letters of Cotton Mather, ed. Kenneth Silverman (Baton Rouge, Louisiana State, 1971), 113–114.
180 Calamy, A Continuation of the Account, 177–211.
181 Charles Morton, Spirit of Man, (Boston, 1692), 63–64; see also the discussion of divine grace on pp. 23–24. See also Norman Fiering, Moral Philosophy at Seventeenth-Century Harvard, 211–227.
182 Calamy, A Continuation of the Account, 191, 200.
183 Calamy, A Continuation of the Account, 200.
184 Morton, A Logick System, 175 of typescript.
185 Calamy, A Continuation of the Account, 206.
186 Morton, A Logick System, 236 of typescript.
187 Morton, A Logick System, 236 of typescript.
188 Charles Morton, Some Meditations on the History Recorded in the First Fourteen Chapters of Exodus, in Meeter (London, date unknown), 10.
189 Calamy, A Continuation of the Account, 192–95.
190 Morison, “Charles Morton,” xviii–xix.
191 Bainbridge Bunting, Harvard: An Architectural History, comp. Margaret Henderson Floyd (Cambridge: Harvard, 1985), 15–16.
192 See Morison, Harvard College in the Seventeenth Century, vol. 2, 490–491.
193 “Diary of Increase Mather,” Proceedings of the Massachusetts Historical Society (1853–58), 317.
194 There is no warrant for Samuel E. Morison’s statement, “it is difficult to find any positive achievement of Mr. Mather’s on behalf of his alma mater,” (Harvard College in the Seventeenth Century, vol. 2, 504). Mather was in charge; he was a patron for both Morton and Brattle, and his own speeches indicate that he was at the forefront of an invigorated humanist atmosphere at Harvard. See Michael Hall’s The Last Puritan: The Life of Increase Mather (Middletown: Wesleyan, 1988), 198–201. For the building program which accompanied the curriculum reform, in part instigated by Morton, see Rick Kennedy, “Thomas Brattle, Mathematician-Architect in the Transition of the New England Mind, 1690–1700,” Winterthur Portfolio 24 (1989): 231–45.
195 Cotton Mather, “An Account of the University,” Magnalia Christi Americana, Bk. 4, Introduction, pt. 2, sect. 6.
196 Samuel E. Morison, “Charles Morton,” xxii.
197 Increase Mather, “The Autobiography of Increase Mather,” American Antiquarian Society Proceedings, New Ser. 71 (1961): 334–335.
198 Morton, Spirit of Man, 12.
199 Morton, Spirit of Man, 87.
200 Ivo Thomas, “Medieval Aftermath: Oxford Logic and Logicians of the Seventeenth Century,” Oxford Studies Presented to Daniel Callus (Oxford: Clarendon, 1964), 297–311. See also Schmitt, John Case and Aristotelianism in Renaissance England, and E.J. Ashworth’s introduction to Robert Sanderson, Logicae Artis Compendium, Language and Logic in the Post-Medieval Period, and Ashworth, “The Eclipse of Medieval Logic,” in The Cambridge History of Later Medieval Philosophy, eds. Norman Kretzman, Anthony Kenney, and Jan Pinborg (Cambridge, England: Cambridge, 1982), 787–796.
201 See W. Henry Kenney, John Locke and the Oxford Training in Logic and Metaphysics (Ph.D. dissertation, Saint Louis University, 1959). John Yolton gives no role to Cartesian or Ramist logic at Oxford in the early eighteenth century; see his “Schoolmen, Logic, and Philosophy,” The History of the University of Oxford, vol. 5, ed. T.H. Aston (Oxford: Clarendon, 1986), 565–593.
202 The two best sources on the eclectic forms of humanistic Aritotelianism are Charles Schmitt’s John Case and Aristotelianism in Renaissance England and books and articles by E.J. Ashworth.
203 Morton, A Logick System, 146 of typescript.
204 For Smith see the Dictionary of National Biography.
205 A bibliography of his textbooks is included in the entry on him in the Dictionary of National Biography.
206 The footnotes to Morton’s Compendium Physicae by Theodore Hornberger indicate the great extent to which Morton relied on LeGrand in that textbook.
207 Morton, A Logick System, 195 of typescript.
208 Arnauld, The Art of Thinking: Port-Royal Logic, “Second Discourse,” 24.
209 Morton, A Logick System, 189 of typescript.
210 Morton, A Logick System, 183 of typescript.
211 See Aristotle, Categoria, 8b. 25–30, 10b. 1–5, trans. E.M. Edghill in The Works of Aristotle, vol. 1, ed. U.D. Ross (Oxford: Clarendon, 1928).
212 Franco Burgersdijck, Institutionum Logicarum, Bk. 1, chap. 6, sect. 4; Robert Sanderson, Logicae Artis Compendium, Bk. 1, chap. 11, sect. 3.
213 Samuel Smith, Aditus ad Logicam, 9th ed. (Oxford, 1684), Bk. 1, chap. 10, 34–36.
214 Coke, The Art of Logick, 33.
215 Morton, A Logick System, 219 of typescript.
216 Melanchthon, Erotemata Dialectices, Bk. 4, especially 642–652.
217 A Defense of the Dissenters Education in their Private Academies (London, 1703), 4.
218 See Clifford K. Shipton, Sibley’s Harvard Graduates, vol. 4 (Cambridge: Harvard, 1933), 201–206.
219 William Brattle, “An Explanation of the Preceding Ephemeris,” An Ephemeris of Cælestial Motions (Cambridge, 1682), first page of essay.
220 Translated by Wilbur S. Howell in Eighteenth-Century British Logic and Rhetoric, 55.
221 Morison, Harvard in the Seventeenth Century, vol. 2, 423.
222 Fiering, Moral Philosophy at Seventeenth-Century Harvard, 241.
223 Nathaniel Mather to Increase Mather, Massachusetts Historical Society Collections, ser. 4, vol. 8, 63.
224 Besides Lynde’s book, Norton’s “Harvard Text-Books and Reference Books of the Seventeenth Century” (p. 402), lists a copy of the Meditations (Amsterdam, 1654) passed between three Harvard students beginning in 1658.
225 Thomas McGahagan, in his Cartesianism in the Netherlands, 1639–1676; The New Science and the Calvinist Counter-Reformation (Ph.D. diss, University of Pennsylvania, 1976), discusses the Cartesian influence on authors popular at Harvard such as Franco Burgersdijck and Adrien Heereboord; however, he writes that “the leading opponents of Cartesianism in the Netherlands were those influenced by English Puritanism” and that “the assumption that Cartesianism was religiously neutral, if not conservative, must be tested against the failure of the anti-Cartesians to see matters so” (2). Brattle’s logic shows that—at least in logic—a very different situation existed in New England. See the comparable reactions to Cartesianism at the universities of Utrecht and Leiden in Theo Verbeek, Descartes and the Dutch: Early Reactions to Cartesian Philosophy 1637–1650 (Carbondale, Il.: Southern Illinois University, 1992), and the Academy in Geneva in Heyd, Between Orthodoxy and The Enlightenment, and Klauber, “Reason, Revelation, and Cartesianism,” 326–339.
226 “Letter of Thomas Brattle,” Narratives of the Witchcraft Cases 1648–1706, ed. George Lincoln Burr (New York: Charles Scribner’s Sons, 1914), 171–172. See also Rick Kennedy, “Thomas Brattle and the Scientific Provincialism of New England, 1680–1713,” The New England Quarterly 63 (1990): 592–594.
227 Mather’s textbook is included in the 1692–1693 notebook of Walter Prince at the American Antiquarian Society; Leverett’s was transcribed in 1720 by Stephen Greenleaf into the notebook of Daniel Greenleaf at the Massachusetts Historical Society.
228 Henry Flynt, “A Particular Account of the Present Stated Excercises Enjoyned the Students,” is printed in Morison’s Harvard College in the Seventeenth Century, vol. 1, 146–147.
229 Quoted in Norton, “Harvard Text-Books and Reference Books of the Seventeenth Century,” 426.
230 John Barnard, “An Autobiographical Fragment,” Congregational Quarterly 4, (1862): 381.
231 Benjamin Rand, “Philosophical Instruction in Harvard University from 1636 to 1900,” Harvard Graduates Magazine 37 (1928–29): 36; see also Thomas Siegel, Governance and Curriculum at Harvard College in the 18th Century, 329, 378–388, for evidence of the use of Locke’s Essay before 1743.
232 See Norman Fiering, “The Transatlantic Republic of Letters: A Note on the Circulation of Learned Periodicals to Early Eighteenth-Century America,” William and Mary Quarterly, ser. 3, 33 (1976): 648–650.
233 See the introduction by J.G.A. Rogers to John Wynne, An Abridgement of Mr. Locke’s Essay Concerning Human Understanding (Bristol: Thoemmes, 1990).
234 The 1758 edition was published by Johanne Draper. Thomas Siegel in Governance and Curriculum at Harvard College in the 18th Century, 277–279, discusses developments in the type and use of textbooks. Siegel in footnotes, 387–388, speculates on the reasons for publication and the possible editors/authors, proposing “Nathan Prince, perhaps with the help of Henry Flynt.”
235 Brattle, Compendium of Logick, 257 of typescript.
236 Brattle, Compendium of Logick, 269 of typescript; and Arnauld, The Art of Thinking: Port-Royal Logic, Bk. 1, chap. 3.
237 Brattle, Compendium of Logick, 269 of typescript, and Blome, 19.
238 Distich in Arnauld, The Art of Thinking: Port-Royal Logic, Bk. 1, chap. 3, 44, and Brattle Compendium of Logick, 270 of typescript.
239 Brattle, Compendium of Logick, 272 of typescript.
240 Brattle, Compendium of Logick, 259 of typescript.
241 Brattle, Compendium of Logick, Bk. 4, chap 2; LeGrand Institutio Bk. 4, chap. 21, sect. 13 (p. 98 of Latin); derived from Arnauld, The Art of Thinking: Port-Royal Logic, Bk. 4, chap. 9, 328. For the best discussion of the method and especially its influence on Locke, see Peter Schouls The Imposition of Method: A Study of Descartes and Locke (Oxford: Clarendon, 1980), 9–21, in which Schouls uses the terms resolution and composition instead of analysis and synthesis.
242 Brattle, Compendium of Logick, “Prolegomenon,” chap. 3, 16; for equivalent, LeGrand, Institutio, Pt. 1, chap. 2, sect. 3.
243 Brattle, Compendium of Logick, “Prolegomenon,” chap. 3, 18; adapted from LeGrand, Institutio Pt. 1, chap. 2, sect. 3–4.
244 Brattle, Compendium of Logick, “Prolegomenon,” chap. 1, 8; for equivalent, LeGrand, Institutio “Prolegomenon,” chap. 1, sect. 13.
245 Descartes, Rules for the Direction of the Mind in Philosophical Writings, vol. 1, 7–78.
246 See the footnote by Dickoff and James in Arnauld, The Art of Thinking: Port-Royal Logic, 302.
247 See especially Arnauld The Art of Thinking: Port-Royal Logic, “Second Discourse [1664], 28, and Bk. 3, chap. 9, 204.
248 Shapiro, Probability and Certainty in Seventeenth-century England: A Study of the Relationships between Natural Science, Religion, History, Law, and Literature (Princeton: Princeton University, 1983), 4–5, 29.
249 Arnauld cites Augustine on “understanding, belief, and opinion” in his “Fourth Set of Objections” (Descartes, Philosophical Writings, vol. 2, 152); in The Art of Thinking: Port-Royal Logic, Bk. 4, chap. 1, 293–94.
250 Brattle, Compendium of Logick, Pt. 3, chap. 3, 166–68; for equivalent, LeGrand, Institutio, Pt. 3, chap. 19, sect. 1–4.
251 Brattle, Compendium of Logick, Pt. 3, chap. 3, 168.
252 Brattle sermon on baptism, date obscured, but probably December 1696, 1. Unless otherwise noted, all Brattle sermons are from the Houghton Library at Harvard University.
253 Bratde sermon, August 26, 1711 PM, 3.
254 Arnauld, The Art of Thinking: Port-Royal Logic, Bk. 4, chap. 1, 298.
255 The doctrine of the Trinity was also taken for granted as divine testimony by LeGrand, Institutio, Pt. 4, chap. 22, sect. 14. Arnauld discusses the Trinity in The Art of Thinking: Port-Royal Logic, Bk. 4, chap. 12, 339.
256 Brattle never offered arguments for the validity of 1 John 5: 7–8; however, he probably agreed with Cotton Mather’s arguments in A Christian Conversation... The Mystery of Trinity (Boston, 1709), 4–6.
257 See Brattle sermon, May 5, 1700.
258 See Edward-Doubleday Harris, An Account of Some of the Descendants of Capt. Thomas Brattle (Boston, 1867), and Rick Kennedy, Thomas and William Brattle in Puritan Massachusetts (Ph.D. diss., University of California, Santa Barbara, 1987).
259 “Diary of John Leverett,” Harvard University Archives, vol. 1, 15.866 vt, 76.
260 See Bernard Bailyn’s The New England Merchants in the Seventeenth Century (Cambridge: Harvard University, 1955) for the classic study of the class to which William Brattle’s family belonged. Bailyn in my opinion applies a paradigm of declining piety among this class too rigidly, especially when dealing with individuals such as Thomas and William Brattle and Samuel Sewall.
261 See Hamilton Andrews Hill, History of Old South Church, 2 vols. (Cambridge: Riverside Press, 1890); and R.G. Pope, The Half Way Covenant: Church Membership in Puritan New England (Princeton, N.J.: Princeton University, 1969).
262 John L. Sibley, Biographical Sketches of Harvard Graduates, vol. 3 (Cambridge, Mass.: Charles W. Sever, Univeristy Bookstore, 1885), 198. Brattle’s manuscript funeral sermon for Oliver is dated April 11, 1703.
263 “Diary of Josiah Cotton,” Publications of the Colonial Society of Massachusetts 26 (1925): 280.
264 Mather, “An Account of the University,” Magnalia Christi Americana, Bk 4, Introduction, pt. 1, sect. 2. See Melanchthon’s declamation, Vita Rodolphi Agricolae, in Corpus Reformatorum: Philippi Melanthonis Opera Quae Supersunt Omnia, ed. Carolus Gottlieb Bretschneider (New York: Johnson Reprint, 1963), 11, 438–446.
265 William Brattle, “An explanation of the preceding ephemeris,” Ephemeris of Cælestial Motions, first page of essay.
266 Benjamin Colman, A Sermon...After the Funerals of..Mr. William Brattle...and...Mr. Ebenezer Pemberton (Boston, 1717), 27.
267 John Wallis to the Bishop of Worcester, June 30, 1699, Royal Society of London, LBC 12.129.
268 See Rick Kennedy, “Thomas Brattle and the Scientific Provincialism of New England, 1680–1713,” 584–600, and “Thomas Brattle, Mathematician-Architect in the Transition of the New England Mind,” 231–245.
269 Morison, “Charles Morton,” xxiv.
270 Puritans discouraged the idea of having chapels with worship services separate from the community church, especially at colleges. Throughout the seventeenth and eighteenth century, Harvard students were to worship at the town meeting house on Sundays, with intermittent sermons given in various places. Holden Chapel was donated to the college and finished in 1742, but served mainly as a lecture hall. There was no official chaplain at Harvard; however, the town minister along with the Hollis Divinity Professor served in the capacity of chaplain.
271 Thomas Siegel and I differ on this point; see his Governance and Curriculum at Harvard College in the Eighteenth Century, 221.
272 Henry Flynt, Diary of Henry Flynt, 1675–1760. Transcribed by Edward Dunn, Harvard University Archives (February 15, 1717), 188.
273 Cotton Mather, Diary of Cotton Mather, vol. 1 (New York: Ungar, American Classics Series, 1957?), 325–26.
274 The nineteenth-century roots of the Brattles-as-liberals tradition are found primarily in two influential books: Josiah Quincy’s The History of Harvard University, vol. 1 (Cambridge: John Owen, 1840), 127, which stated that the Brattles and Leverett “were not adherents to the rigid doctrines” of the early established Congregational Church of New England, and Samuel Kirkland Lathrop’s A History of the Church in Brattle Street, Boston (Boston: W.M. Crosby and H.P. Nichols, 1851), 16, 18, which contrasted the “free air of the wilderness” breathed by the Brattles with the “ignorance and prejudice” of the Mathers. These interpretations influenced John L. Sibley, see his Biographical Sketches of Graduates of Harvard University, which became the standard reference work on the Brattles, Leverett, and people associated with Harvard in the seventeenth century. Many recent historians, no longer harboring antagonism to the Mathers, still tend to rely on traditional viewpoints drawn from Quincy and Lathrop. John Corrigan’s The Prism of Piety: Catholick Congregational Clergy at the Beginning of the Enlightenment (New York: Oxford, 1991), 17–27, is the most recent work on the subject from the traditional perspective.
275 Letter from Lord Bellomont to Samuel Sewall, 17 August 1700, Records Commission of Boston (Boston, 1917), ser. 2, vol. 2, 139–40.
276 “Draft of a Letter from Increase Mather to the Speaker of the House,” October, 1702, Publications of the Colonial Society of Massachusetts 49 (1975), 195–96.
277 Mather’s support for Brattle’s presidency is the context of Brattle’s letter to Mather, as found in Publications of the Colonial Society of Massachusetts 49 (1975): 218.
278 Mather’s eulogy for Brattle is in the preface to Joseph Sewall’s sermon Precious Treasure in Earthen Vessels (Boston, 1717). William Brattle’s will is published in Edward-Doubleday Harris, An Account of the Descendants of Capt. Thomas Brattle, 17–25.
279 Cotton Mather, “An Account of the University,” Magnalia Christi Americana, Bk 4, pt. 1, sect. 6.
280 Harry S. Stout, The New Engand Soul: Preaching and Religious Culture in Colonial New England (New York: Oxford, 1989), 131–160.
281 Colman, A Sermon...After the Funerals of…Mr. William Brattle...and...Mr. Ebenezer Pemberton, 36.
282 See Stout, The New England Soul, 106–111. See also David D. Hall, The Faithful Shepherd: A History of the New England Ministry in the Seventeenth Century (Chapel Hill: University of North Carolina for the Institute of Early American History and Culture, 1972).
283 John Corrigan, The Hidden Balance: Religion and Social Theories of Charles Chauncy and Jonathan Mayhew (Cambridge: Cambridge, 1987), 38.
284 Joseph Stevens, Another and Better Country. . . To which is added a discourse, had by him at Cambridge after the Death of the late Reverend Mr. Brattle (Boston, 1723).
285 Morison, Harvard College in the Seventeenth Century, vol. 2, 470–71; Letter to the Bishop of London, Fulham Palace Mss, Archives of the Bishop of London, Lambeth Palace Library, London (transcipts are in the Library of Congress), box 4, 35–36.
286 Henry Newman to Dr. Smallridge, 9 March 1713/14, Society Letters, CS2/4, p. 18 in the archives of the Society for the Promotion of Christian Knowledge (SPCK), London.
287 See Leonard W. Cowie, Henry Newman: An American in London 1708–1743 (London: SPCK, 1956).
288 Newman to Smallridge, 18. See also Newman to Mr. Taylor, March 29, 1714, SPCK, Society’s Letters, CS2/4, 31–32.
289 Henry Newman to Benjamin Colman, October 20, 1722, SPCK, New England Letter Book, CN3/1, vol. 1.
290 Quoted in Arthur Kaledin, The Mind of John Leverett (Ph.D. dissertation, Harvard University, 1965), 248.
291 William Brattle to Mr. Dudley, 18 November 1700, Massachusetts Historical Society, C. E. French manuscripts.
292 Brattle sermon, March 16, 1700.
293 Sibley, Biographical Sketches of Harvard Graduates, vol. 3, 201.
294 Sewall, Diary of Samuel Sewall, vol. 2, 846.
295 Sibley, Biographical Sketches of Harvard Graduates, vol. 3, 203–204.
296 Colman, A Sermon...after the Funerals, 35; and Sewall, Diary of Samuel Sewall, vol. 1, 449.
297 Brattle sermon, 10 March 1705–6, p. 6, Houghton Library, Harvard University, MS Am 1100.
298 Brattle sermon on James 5:16, c. April, 1712, p. 4.
299 Brattle sermon on James 5:16.
300 Sibley, Biographical Sketches of Harvard Graduates, vol. 3, 204.
301 See Edward Dunn’s Henry Flynt, and Shipton, Sibley’s Harvard Graduates, vol. 4, 162–167.
302 Brattle sermon, February 18, 1704 on Jude: 3, p. 1.
303 Brattle sermon, May 5, 1700, on James 4: 17, p. 5.
304 Ebenezer Turell, The Life and Character of the Reverend Benjamin Colman (Boston, 1749), 55.
305 That Wigglesworth was probably the main author of The Testimony, I assume, since he wrote A Letter to the Reverend Mr. Whitefield by way of Reply to his Answer to the College Testimony Against him and his Conduct (Boston, 1745), which reiterated the Lockean condemnation of his “enthusiasm.”
306 The Testimony of the President, Professor, Tutors and Hebrew Instructor of Harvard College (Boston, 1744), 4. In New England’s Great Awakening, such testing of the strong affections was also a theme of Jonathan Edwards’ A Treatise Concerning Religious Affections, preached in 1741–1742 and published in 1746.
307 Wigglesworth, The Sovereignty of God, (Boston, 1741), 6.
308 Wigglesworth, A Seasonable Caveat, (Boston, 1735), 5.
309 Wigglesworth, A Seasonable Caveat, 9–10.
310 Edward Wigglesworth, An Enquiry into the Truths of the Imputation of the Guilt of Adam’s First Sin to his Posterity (Boston, 1738), “preface,” n.p.
311 John Barnard, “Autobiography of John Barnard,” Collections of the Massachusetts Historical Society, ser. 3, 5 (1836): 182.
312 Sibley, Biographical Sketches of Harvard Graduates, vol. 3, 204.
313 Barnard, “Autobiography of John Barnard,” 186.
314 Shipton, Sibley’s Harvard Graduates, vol. 4, 501–514.
315 See Norman Fiering, Jonathan Edwards’s Moral Thought, 33–34, where he discusses Williams’s use of The Port-Royal Logic and notes that Yale’s use of a logic in the senior year was odd but indicates the possibility that Arnauld’s text might have been used in moral philosophy or even as a capstone book in that it encompassed much of what had gone before it in the curriculum. See the biographical sketch of Williams in Shipton, Sibley’s Harvard Graduates, vol. 5, 588–98.
316 Jonathan Mayhew, “Notes on Pascal” (Mayhew Papers, Special Collections, Mugar Memorial Libary, Boston University), 3.
317 Brattle sermon, Prov. 10: 9, c. March 1705/6.
318 “Letter of Thomas Brattle,” 182
319 “Letter of Thomas Brattle,” 182–83.
320 “Letter of Thomas Brattle,” 183, 186.
321 The 1766–1767 curriculum reform is discussed in Siegel, Governance and Curriculum at Harvard College in the 18th Century, 123, and Condy’s bookshop analysis is 312–314, especially 314n.
322 See Rand, “Philosophical Instruction in Harvard University From 1636 to 1900,” 40–43.
323 The Centinel, March 20, 1816. Harvard University Archives (HUG 300).
324 Levi Hedge, Elements of Logick (Cooperstown, 1843), 92.
325 Hedge, Elements of Logick, 100.
326 See Morison, Three Centuries at Harvard, 187–191; Conrad Wright, “Early Years of the Divinity School,” Harvard Alumni Bulletin (March 20, 1954), n.p; and William Warren Sweet, “The Rise of Theological Schools in America,” Church History 6 (1937): 260–273; and Mark A. Noll, Princeton and the Republic, 1768–1822 (Princeton, N.J.: Princeton, 1989).
327 Kelly James Clark, Return to Reason: A Critique of Enlightenment Evidentialism and a Defense of Reason and Belief in God (Grand Rapids: Wm. B. Eerdmans, 1990).
328 I confess not to know much about logic in American Roman Catholic colleges; however, Christopher Derrick in Escape From Scepticism: Liberal Education as if Truth Mattered (Peru: Sherwood Sugden, 1977), using the example of Thomas Aquinas College in California, advocates an Augustinian-based Thomism as the best epistemology for liberal education. As in the seventeenth-century, dogmatically-oriented Protestants and Roman Catholics can still share fundamental epistemological views.
1 Francis Bacon (1561–1626) published in English his The Great Instauration and The Advancement of Learning. Kenelm Digby (1603–1665), Henry More (1614–1687), and John Wilkins (1614–1672) wrote many works in English. “Raynolds” might be Richard Rainolde (d. 1606) who wrote a rhetoric textbook in English, but the book does not seem to have been popular after its publication in 1563. I have not been able to find “Beylo,” or some name like it, but suspect it might be one of the pseudonymns attached to Thomas White (1593–1676) who wrote several philosophical works in English, including Controversy-Logicke, or the Method to come to Truth in Debates of Religion (1659). White’s most common alias was Blacklo.
2 Dunbar’s version calls this simply “mathematicks.”
3 Porphyry (b. 232/233 AD) was a pro-Aristotelian and anti-Christian logician who was influential in neo-Platonic education. St. Augustine praised Porphyry forimproving “upon both Plato and Plotinus.” The “tree” seems to have been a later development by those teaching from Porphyry’s hagoge and his two commentaries on Aristotle’s Categories. See Christos Evangeliou, Aristotle’s Categories and Porphyry (Leiden: E.J. Brill, 1988) and Porphyry: On Aristotle’s Categories, trans. Steven K. Strange (Ithaca: Cornell, 1992).
4 Partridge makes a mistake here by extending the Predicamentalls bracket to include “man.” He does not do it in chapter 2, nor does Dunbar in his version.
5 Dunbar’s transcription has “Smith’s, Sanderson’s, Bergersdicius his logick.” The Smith mentioned is probably Samuel Smith’s Aditus ad Logkam (London, 1613) which was popular at Oxford for most of the seventeenth century. See Wilbur S. Howell, Logic and Rhetoric in England 1500–1700, 292–299 for a discussion of Smith’s logic. The other neo-Aristotelian sources are Robert Sanderson’s Logicae Artis Compendium (Oxford, 1615) and Franco Burgersdijck’s Institutionum Logicarum (Cambridge, 1647).
6 Lines such as this indicate copying a portion of the sentence above.
7 Partridge’s use of brackets and parentheses is erratic.
8 Although rooted in Aristotle’s Categoriae, chapter. 2, this discussion of predicables is highly influenced by early Medieval developments which William and Martha Kneale in The Development of Logic, 187, think might be rooted in Porphyry’s Isagoge, principally the quinque voces of species, genus, differentia, property, and accident. Morton’s use of “Porphyry’s Tree” and neo-Aristotelianism’s general use of predicables as discussed here indicates an acceptance of post-Aristotelian developments by humanistic logicians even though their rhetoric emphasized purifying Aristotelianism of its Medieval accumulations. Such reliance on post-Aristotelian developments is evident throughout A Logick System.
9 ![]() is a symbol for the Latin recipere which means to receive. Used mosdy by physicians since the Middle Ages, the use here to delineate rules is an idiosyncrasy.
is a symbol for the Latin recipere which means to receive. Used mosdy by physicians since the Middle Ages, the use here to delineate rules is an idiosyncrasy.
10 Predicament is another name for category.
11 Morton’s understanding of spiritual substance has far reaching consequences on his understanding of human procreation. In the Compendium Physicae, 143, Morton wrote against “the Antients” who believed the male seed “active” and female “passive.” Morton insisted on “spirituous matter” in both male and female that is “conjoyn’d” along with “grosser matter” to produce a child.
12 The penetrability of spiritual substance is extensively discussed by Henry More in several works, especially The Immortality of the Soul. The parenthetical remark comes from Mark 5: 1–20 where Jesus asks a demon-possessed man his name and the evil spirits reply “My name is Legion for we are many.”
13 The extent of infusion in Bezaliel and Aholiab is clear in Exodus 35: 30–35: God filled Bezaliel “with an excellent spirit of wisdom, of understanding, and of knowledge in all manner of work, to find out curious works, to work in gold, and in silver, and in brass, and...to make any manner of fine work. And [God] hath put in his heart that he may teach others, both he and Aholiab....Them hath he filled with wisdom of heart to work all manner of cunning embroidered and needlework....” Prof. Morris Wilhelm helped me read these names and directed me to the book of Exodus.
14 Although awkwardly stated here, this Aristotelian adage (An obstinate skeptic cannot be argued with) was commonly used against skeptics by all forms of dogmatically-inclined humanistic logics.
15 Dunbar mistakenly positions the “active” and “passive” under the operative definition.
16 Dunbar mistakenly positions “virtue” and “vice” under infused habits.
17 “Of or pertaining to a master,” OED.
18 This sentence is not completely transcribed by Partridge.
19 The followers of King David in exile expressed their need for their leader with this formula.
20 “Put” should be “But.”
21 This is a favorable nod to Ramists.
22 Partridge mistakenly wrote “parts in” twice.
23 A reference to Antoine Arnauld’s The Port-Royal Logic.
24 AEIO was a popular designation for the four types of propositions. Since a syllogism contains three propositions and four types for each, there are 4 × 4 × 4 or sixty-four possible modes.
25 E. is an abbreviation for Ergo.
26 The “Memoriall Verses” has “three” instead of “the.”
27 This Medieval memory device probably was not cabbalistical. The oldest known version is in William of Shyreswood’s Introductiones in Logicam written in the first half of the thirteenth century. For a more complete discussion of moods and figures using this device, see William of Sherwood’s Introduction to Logic, trans. Norman Kretzmann (Minneapolis: Minnisota, 1966), 60–68. Morton’s trimmed down and perfunctory explanation of these important aspects of scholastic syllogistic logic is consistent with the general lack of interest and competence in humanistic logic.
28 The “Memorial Verses” has “mean” instead of “main.”
29 “For the invisible things of him, that is his eternal power and Godhead, are seen by the creation of the world....”
30 The “Memorial Verses” has “has no.”
31 Tautology or circular reasoning.
32 Matt 16:18.
33 Partridge mistakenly wrote “body mind” when he meant to write just “mind.”
34 Geneva Bible: “...delivered from unreasonable and evil men: for all men have not faith.” The “unreasonable and evil” in Greek is atomos which can be translat ed as “without topic” as Morton says. “Out of place,” or “improper” might make more sense as a literal translation today. Tim Vivian provided this information to me.
35 The “Memoriall Verses” has “whence they are sought.”
36 Dunbar’s version has “Physician” here.
37 Rational.
38 Quakers, the Society of Friends, emphasized the inner light from the Holy Spirit more than Puritans. Puritans, in general, were antagonistic to Quakerism, insisting that it was a form of antinomianism and fanaticism. Puritans and Quakers shared the role of dissenters in late seventeenth-century Britain, but Puritans were especially sensitive to making a clear distinction between their form of rational religion and the Quakers’ form of pietism.
39 Both Dunbar and Partridge transcribe “of” instead of “off.” This is an indicator of the mindlessness of transcription and the way an error may spread through various branches of transcriptions.
40 It is tempting to assign this example to the particular problem of dissenters in Britain (especially applicable to New England after its corporate charter was revoked). Puritan churches and corporations were legally repressed and forced to give up “conveniences” that would normally have been their legal right. Morton, however, takes the view of the universal church and the whole commonwealth here rather than the particular church and corporation that suffer being cut and plucked. Statements such as this in the textbook would have been excellent for inciting classroom discussion of Puritan politics and religion.
41 It is not whether clear Morton meant exact ratios here. He does, however, repeat this formula twice more. Possible applications of mathematics to testimony was an exciting area of study in the late seventeenth century. C.A.J. Coady in Testimony: A Philosophical Study (Oxford: Clarendon, 1992) devotes a chapter to post-Lockean mathematical calculations of the rate of diminishing credibility in testimony, leading to predictions of when a particular testimony (such as the New Testament) would have no credibility. One anonymously written study, “A Calculation of the Credibility of Human Testimony” in Miscellanea Curiousa... being the most valuable Discourses, Read and delivered to the Royal Society, (1708), 3, 1–8, for example computes: “If two concurrent reporters have, each of them, as 5/6ths certainty, they will both give me an assurance of 35/36ths, or 35 to one: If three: an assurance of 215/216, or 215 to one” (p. 4).
42 Dunbar’s version has “compared” which is what partridge probably meant to write.
43 This distich does not appear in the “Memorial Verses.”
44 Johann Clauberg (1622–1655) was an influential German educational reformer and philosopher. Brattle, following The Port-Royal Logic, cites the model of Clauberg’s Logica Vetus et Nova (Amsterdam, 1654).
45 Actually 5 times read if you count the summary scheme and Memorial Verses which follow this.
1 In text: “Spirit & Body Substance & Species”
2 In text: “Continual Quantity, is Long, Broad Thick”
3 In Text: “parteth Generall”
4 Partridge wrongly transcribed this line. It should end with “Implied.”
1 These rules are derived from LeGrand’s Institutio.
2 This passage is directly from LeGrand’s Institutio, Pt. 1, chap. 2, reg. I.V. LeGrand goes on to give a title for Aristotle’s chapter: “Of the Usefulness of Doubting, and what things we ought first to doubt of” (trans. Blome, 5).
3 Pages cited are to the present transcription.
4 Ens means something that has existence or being.
5 The only reference I have found to Brattle’s Compendium in philosophical literature is a footnote reference to this distich in Abraham Edel’s “Aristotle’s Categories and the Nature of Categorical Theory,” The Review of Metaphysics 29 (1975): 59. Edel states that these seven heads instead of the Aristotelian ten are “particularly significant” for “the substitution of matter for the Aristotelian substance, the mathematical emphasis in measure, and the similarity of the remaining categories to Locke’s primary qualities. Aristotle’s category of quality is explicitly reduced to the effects of figure and motion, but mind is regarded as irreducible, a category distinct from all material ideas.” Edel points out the important difference with Aristotelian logic here; however, he is wrong to see Locke’s influence. The distich comes from early seventeenth-century Dutch Cartesianism. See Theo Verbeek, Descartes and the Dutch: Early Reactions to Cartesian Philosophy, 1637–1650 (Carbondale: Southern Illinois, 1992): 14.
6 Sir Kenelm Digby (1603–1665). See the discussion of his influence and other Roman Catholic Aristotelians on Charles Morton in Kennedy’s “Humanism, Religion, and Dogmatism.” Digby first had great hopes for Cartesianism before returning to an emphasis on Aristotelianism.
7 Kenelm Digby, A Treatise of the Nature of Bodies, first published in Paris in 1644 with three subsequent London editions, the last in 1669.
8 These long sections from Digby are not derived from LeGrand’s Institutio or Arnauld’s The Port-Royal Logic. Neither of those books have this argument that the neo-Aristotelian use (i.e. Morton’s use) of the ten predicaments is not to be found in Aristotle. Although the ten predicaments had been revised and standardized during the Middle Ages, Digby and Bratde make a weak argument.
9 A Quality is that whereby a substance is denominated such a kind.
10 Note the separation of extended substance from thinking substance. Morton insisted that spiritual/thinking substance is also extended, but is penetrable. See Morton A Logick System, Pt. 1, chap. 6, (p. 163 of typescript).
11 This page reference refers to LeGrand’s Institutio, 1680 edition, Pt. 1, chap. 4.
12 LeGrand’s Institutio, Pt. 1, chap. 9.
13 LeGrand’s Institutio (1680 edition), Pt. 1, chap. 9.29.
14 Brattle begins his logic strictly in English, following the ideal presented in Morton’s preface. From here on he increasingly becomes lazy in translating Latin terms and sentences.
15 LeGrand’s Institutio (1680 edition). Ars Cogitandi is more commonly called The Port-Royal Logic.
16 God exists i.e. is existing. God loves humans, i.e. is loving humans.
17 The “sum” in the Cogito—“I think, therefore I am”—means more fully “Ego sum ens” or “therefore, I am a being.”
18 Brattle takes this section from Arnauld’s The Port-Royal Logic, Bk. 2, chap. 5. It is interesting but trivial to note that the Bible does not quote Jesus making the exact phrase “He who does the will of my father who is in heaven shall enter into the kingdom of heaven.” One would think that Arnauld’s Jansenism and Brattle’s Puritanism would have alerted them to a phrase that appears outside the border of each man’s theology of salvation. Jesus’s parable of the two sons (Matt. 21: 28–31) seems to be the closest source.
19 Goods and evils come from God.
20 The invisible God (Or God who is invisible) created the visible world (or world that is visible).
21 (Horace, Epodes 2.1–4), translated by James Dickoff and Patricia James in The Art of Thinking, 116, as “Happy he who like the ancient mortal race / Far from commerce and from trade / Tills with beast the ancestral fields, / From all negotiations free.”
22 Brattle introduced the example of Aeneas’ fame but copied the example of God punishing the oppressors of the poor from Arnauld’s The Port-Royal Logic, Bk. 2, chap. 5.
23 (Virgil Aeneid 1.1a–d, 1–3). Dickoff and James in The Art of Thinking, 117, trans late this: “I, who once tuned my song to a slender reed / But then left the wood land, bidding the neighboring fields / To serve the landsman, however demanding, / A servitude welcome to farmers, sing of Mars-bristling / Arms now and the man who once from the coast of Troy / Exiled by Fate to Italy and Lavinian Shores first came.”
24 Brattle jumps from chapter five to chapter eight in The Port-Royal Logic, Bk. 2, for this section and Latin examples of asserting the roundness of the Earth and that Astronomers have reasons when they convince us that the Sun is much bigger than the Earth.
25 “All philosophers teach that heavy things fall of their own accord.”
26 “Now stones are heavy things, therefore, they fall of their own accord.”
27 “But that is false; therefore it is possible that something false be taught by all philosophers.”
28 Arnauld’s The Port-Royal Logic, Bk. 2, chap. 8, goes on to give the aeio and explain the mnemonic words that go along with it. Brattle will give the aeio later.
29 Brattle backtracks to The Port-Royal Logic, chap 6, for this section. The Latin: “men who are created to know and love God; or men who are pious.”
30 Partridge uses the spelling “misrecordes” but Jeffries and Dunbar used “misericordes.” The term means merciful or charitable; therefore, the Latin: “men who are pious are...”
31 Men in general.
32 Dickoff and James translate this in The Art of Thinking, 119: “The doctrine which identifies the sovereign good with the sensual pleasure of the body and which was taught by Epicurus is unworthy of a philosopher.”
33 Brattle takes this chapter from Arnauld’s The Port-Royal Logic, Bk. 2, chap. 9. The Latin: “Knowledge and riches will not make one happy.... Knowledge and riches make one vain.”
34 Example 1, that death and life are in the hands of the tongue, is from Arnauld’s The Port-Royal Logic, Bk. 2, chap. 9; however, Brattle chooses his own examples for 2, “a person has life and reason,” and 3 “humans and angels exist and are created.”
35 This phrase, “Faith and good works are necessary for salvation,” is used by both Arnauld and Brattle and derived from James 2: 14–26.
36 (P. Syrus, Sententiae 25) translated by Dickoff and James in The Art of Thinking, 129: “Friendship either finds friends equal or makes them so.”
37 These examples are from Arnauld’s The Port-Royal Logic: “If the earth is stationary, then the sun moves; If God is just, then evil is punished.”
38 “If death is the transition to the happy life, death is to be desired.” I have not been able to find which edition Brattle is citing.
39 Dickoff and James in The Art of Thinking, 131, translate this: “If the will of the creature is capable of keeping the absolute will of God from being accomplished, then god is not omnipotent.” This example was a fundamental premise in the logic of Christians who insisted on predestination.
40 Brattle mixes three examples, apparently well known to his students. Dickoff and James in The Art of Thinking, 132, translate them: “Woe to the rich, because they have their comfort in this world. The wicked are exalted that, falling from a greater height, their demise may be the greater. (Claudian, In Rufinum 1. 22–23) They are able, because they believe themselves able. (Virgil, Aeneid 5.231.)
41 “Men in general are rational; kings as kings depend on God alone.”
42 Dickoff and James in The Art of Thinking, 133, translate these three: “Where one’s treasure is, there is his heart. As a man lives, so he dies. You are valued in the world in proportion to your wealth” (Seneca Epistles 65.14).
43 But or however, nevertheless or yet.
44 Dunbar and Jeffries have these three examples in a different order; however, Patridge’s order follows The Port-Royal Logic. Dickoff and James translate these three classic adages in The Art of Thinking, 134: “Fortune can take away one’s goods, but it cannot take away one’s heart. (Seneca, Medea 176) Rather than being a victim of my circumstances, I try always to rise above them. (Horace, Epistles, 1.1.19) He who crosses the seas changes only his county, not his disposition” (Ibid., 11.27).
45 This example from John 12: 3–5 is translated by Dickoff and James in The Art of Thinking, 134: “Judas was a theif, and nevertheless he could not abide Magdalene’s pouring her ointments on Christ.”
46 All the manuscript logics transcribe this wrong reference. Chapter eight should be chapter ten of The Port-Royal Logic, Bk. 2.
47 Although the chapter uses a title similar to The Port-Royal Logic, Bk. 2, chap. 4, Brattle here draws mainly from LeGrand’s Institutio, Pt. 2, chap. 13.
48 This example does not appear in either The Port-Royal Logic or the Institutio; however, it does appear in a similar section in Morton’s A Logick System, Pt. 2, chap. 3.
49 This or that man is just.
50 “All viscious people are slaves. No viscious people are happy. Some viscious persons are rich. Some viscious persons are not rich.”
51 The distich is given in Arnauld’s The Port-Royal Logic, Bk. 2, chap. 3: “both are general” or “both particular.”
52 Opulentus means splendidly rich.
53 “All intellectual substance is thinking substance / mind is intellectual substance, / therefore mind is thinking substance.”
54 “All pious kings are loved by their subjects.”
55 Dickoff and James in The Art of Thinking, 178, translate this as “If an elective state is subject to division, the state is not of long duration. / But an elective state is subject to division. / Therefore, an elective state is not of long duration.”
56 Dickoff and James in The Art of Thinking, 179, translate this as “The divine law binds us to honor kings. / Louis xiv is king. / Therefore, the divine law binds us to honor Louis xiv.” LeGrand, in the Institutio, when he takes this example from The Port-Royal Logic, changes the king to Charles II. LeGrand obviously believed such changes would help with the acceptance of his logic. Brattle does not seem to have been concerned with such changes.
57 This example from LeGrand’s Institutio, Pt. 1, chap. 16. Fernelius is the name of a physician.
58 The Port-Royal Logic, Bk. 3, chap. 3, names the same three that Brattle names.
59 Both The Port-Royal Logic, Pt. 3, chap. 5, and the Institutio, Pt. 1, chap. 16, teach this memory device.
60 Saxum means rock.
61 Here again is the assertion of spiritual substance that is not material.
62 Lapis is a stone.
63 Jews, being usurers, will not be saved.
64 Infinite divisibility was a conundrum often pondered and disputed in the second half of the seventeenth century.
65 “Mind is not body, and the body is not receptive to perceptions. It does not follow that the mind is receptive to perceptions.”
66 “That one man has surrendered to wine does not mean that all men have surrendered to wine.”
67 “If the human mind be corporeal, it can be divided into parts. / But in fact human minds are not able to be divided into parts; therefore / human minds are not corporeal.”
68 “If every created thing cannot subsist through itself, it is necessary that they subsist through God. / Indeed, every created thing cannot subsist through itself therefore, / it is necessary that they subsist through God.”
69 Loosely: “an antecedent must be followed by a consequent.”
70 “If John is married to this wife, he acts foolishly, / But John does not act foolishly, therefore / he is not married to this wife.”
71 “If a stone is living, it is a substance.”
72 “A body is not able to be a plane and round at the same time / but the earth is round, therefore / the earth is not a plane.”
73 “Human death happens either to the corrupt soul or body, / but it does not happen to the corrupt soul, therefore / it happens to the corrupt body.”
74 “Those who first reported to us that antipodes existed either were telling the truth or were imposing upon our credulity, / but they were telling the truth, therefore / they were not imposing upon us.” Jeffrey B. Russell in Inventing the Flat Earth (New York: Praeger, 1991), discusses the significance of knowledge of the Antipodes in history which were considered the opposite quarter of the Earth.
75 Loosely: “It is impossible for contradictories to be both true at the same time.”
76 “2:4 = 3:6 = 4:8 = 6:12 therefore 2:8 = 3:12”
77 “He who is powerful enough to save you is powerful enough to destroy you. / Now I am powerful enough to liberate you, and therefore to destroy you.”
78 “This triangle...and that triangle..., and so do the rest; therefore, all triangles have three lines.”
79 “Caesar controlled the Roman people through clemency more than through arms….Thus a ruler ought to resort to clemency rather than to arms in order to subdue his people.”
80 “The avaricious are very greedy; those who are very greedy desire many things; those who desire many things are miserable; therefore, the avaricious are miserable.”
81 “Salty meat makes one desire to drink; drinking solves the problem; therefore, salty meat was the problem to be solved.”
82 “Either you know you have disobeyed the king’s law or not. If you know you have, who are you to have dared to disobey the king’s law? But if not, why, once the crime has been committed, do you throw yourself down to be trampled?”
83 The Port-Royal Logic, Pt. 3, chap. 16, the Institutio, Pt. 1, chap. 19, and Morton’s A Logick System, Pt. 3, chap. 2, (p. o) all use similar examples for this type of dilemma: “Either a wife is beautiful or ugly, if beautiful then she incites jealousy; if ugly she will displease. Therefore, one should not marry a wife.”
84 “Some women are not so beautiful so as to incite jealousy nor so ugly so as to displease.”
85 “Either a thing pleases or it does not.”
86 Persuasive.
87 The Institutio, Pt. 1, chap. 19.13, has “Spectatissimus,” meaning a precise astronomer or careful sky-gazer.
88 “All lines between two points are equal, / Now a straight line and a slanting line run from the same point to the same point, / Therefore the straight and slanting lines are equal.”
89 “Whatever you haven’t lost, you have. / If you haven’t lost your wife, you have a wife.”
90 “Truth incites hatred, / A lie incites hatred, Therefore / truth is a lie.”
91 “Whatever you haven’t lost, you have, / But your hat (which once was lost but now is found) you have, Therefore / You haven’t lost that hat.”
92 The Port-Royal Logic, Bk. 3, chap. 19.
93 “The blind see, ie. those who were once blind and not able to see, now see.”
94 Confusing a qualified truth to a truth.
95 These criticisms and the praise for Johann Clauberg’s Logicae, Vetus et Nova (1654) come from The Port-Royal Logic, Pt. 3, chap. 18.
96 Dickoff and James in The Art of Thinking, 241, translate this as “Whatever is affirmed or denied of the genus is affirmed or denied of the species. What belongs to all men belongs to great men.”
97 Dickoff and James in The Art of Thinking, 241, translate this as “In denying the genus, we also deny the species: He who does not judge does not judge ill.”
98 Dickoff and James in The Art of Thinking, 241, translate this as “In denying the species, we deny the genus: ‘Substantial’ forms (except the rational soul) are neither body nor spirit; therefore, these forms are not substances.”
99 Dickoff and James in The Art of Thinking, 241, translate this as “If we affirm or deny a difference, then we affirm or deny the corresponding species: Extension does not belong to thought, thought is not matter.”
100 Dickoff and James in The Art of Thinking, 242, translate that as “If we can affirm or deny the essential attribute then we can affirm or deny the species: It is impossible to imagine half a thought, or a round thought, or a square one; so thought cannot be body.”
101 Dickoff and James in The Art of Thinking, 242, translate this as “We affirm or deny what is expressed by the defined word when we affirm or deny what is expressed by the defining words: Few persons are just, because few persons have the firm and abiding will to give to each what is due.”
102 “Cause, effect, whole, part, opposition.”
103 “2 × 4 = 8, 3 is a number.”
104 Brattle and LeGrand both follow The Port-Royal Logic, Bk. 4, chap. 2, on the use of logic in this example. Dickoff and James in The Art of Thinking, 307, translate this, “Strictly speaking, we may say that no substance perishes. / What is called destruction is only a rearrangement of parts. Therefore, what has not parts cannot be destroyed.”
105 Logic textbooks often used this analogy of climbing and descending a mountain which, to my knowledge, was first given in The Port-Royal Logic, Bk. 4, chap. 2. Arnauld gave two analogies, one geneological and the other ambulatory. The geneological never caught on. The image of climbing a mountain in pursuit of Truth was increasingly used in the late seventeenth century.
106 Partridge fills the bottom of the final page with a design around this distich.